1.69
题目
Let
a. Show that for each
b. Describe a much smaller NFA for
思路
点击展开
a. Myhill–Nerode theorem 秒杀
b. NFA 刻画可能性,善于直接刻画存在性问题
所以我们为每个
解答
点击展开
a.
b. 当
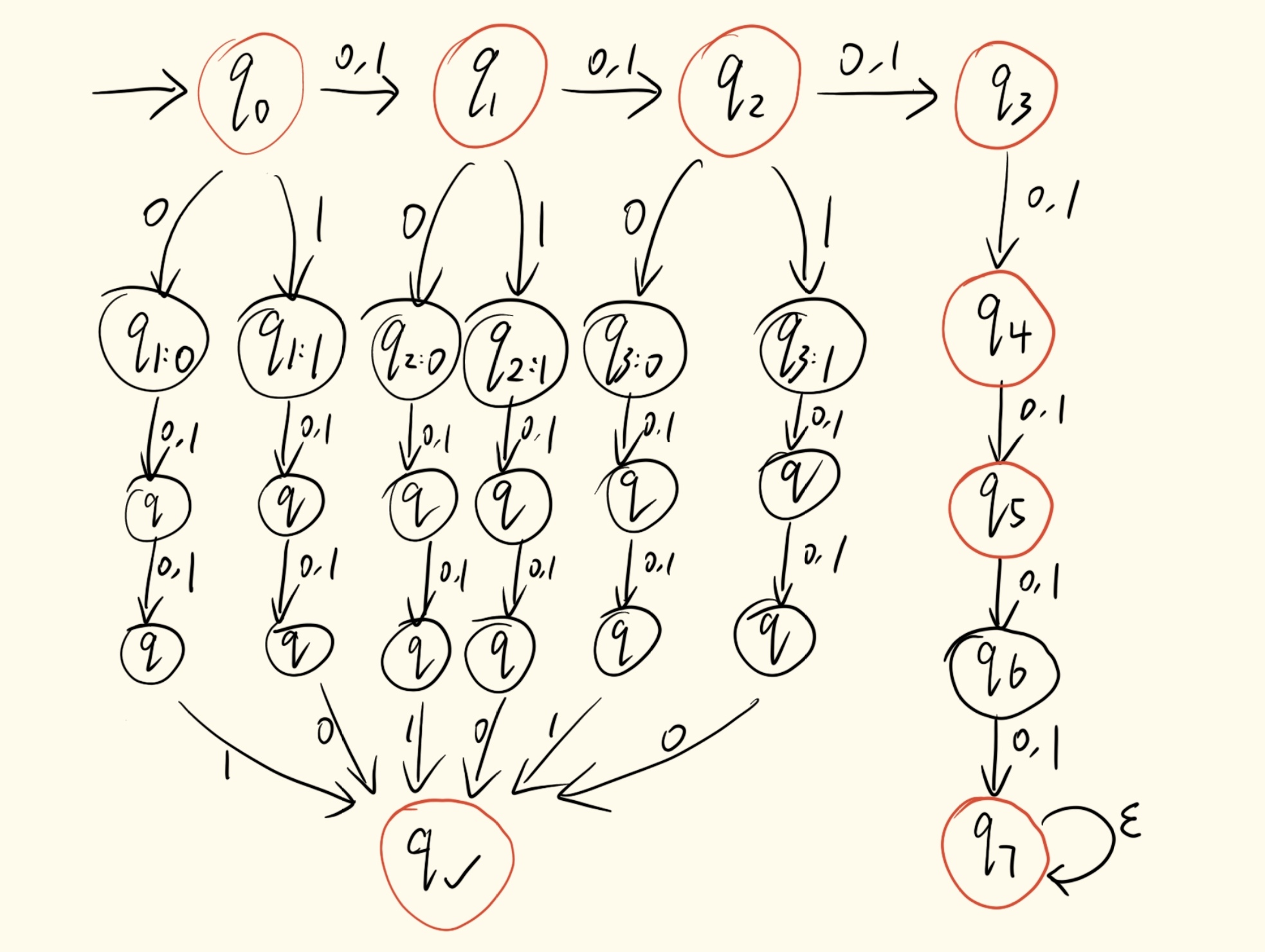
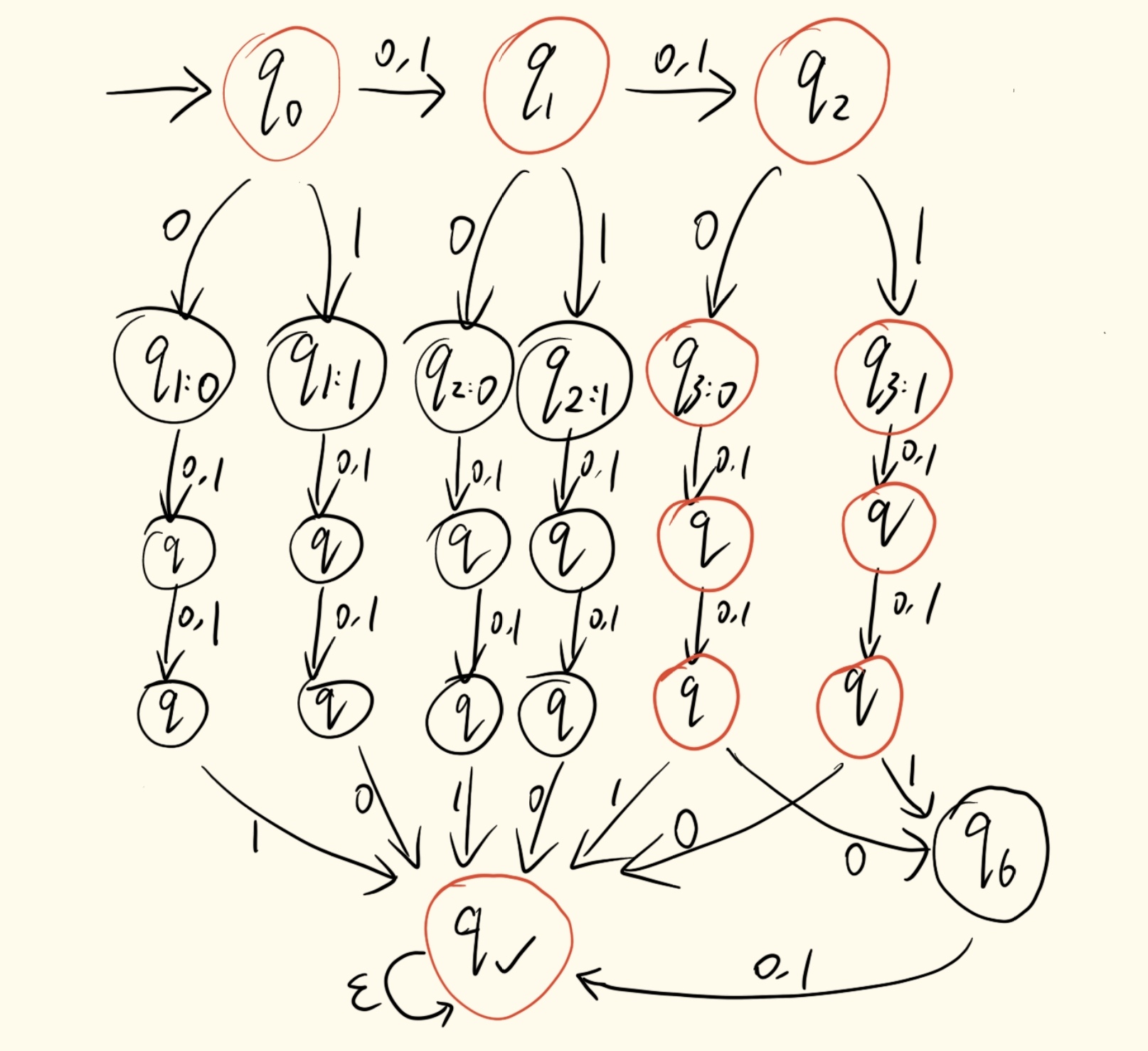
一般地,需要至多
Let
a. Show that for each
b. Describe a much smaller NFA for
a. Myhill–Nerode theorem 秒杀
b. NFA 刻画可能性,善于直接刻画存在性问题
所以我们为每个
a.
b. 当


一般地,需要至多